Statement/Propositions
A statement or a proposition, is a declarative sentence that is either TRUE or FALSE, but not both.
Example: • 4 is less than 3. • 7 is an even integer.
• Washington, DC, is the capital of United State.
i) Why do we study mathematics?
ii) Study logic.
iii) What is your name?
iv) Quiet, please.
The above sentences are not propositions.
Why ?
(i) & (iii) : is question, not a statement.
(ii)& (iv) : is a command.
Disjunction
Let p and q be propositions.
• The disjunction of p and q, written p∨q is the statement formed by putting statements p and q together using the word “or”.
• The symbol ∨ is called “or”.
i) p: 2 is an integer ; q: 3 is greater than 5 p∨q = 2 is an integer or 3 is greater than 5
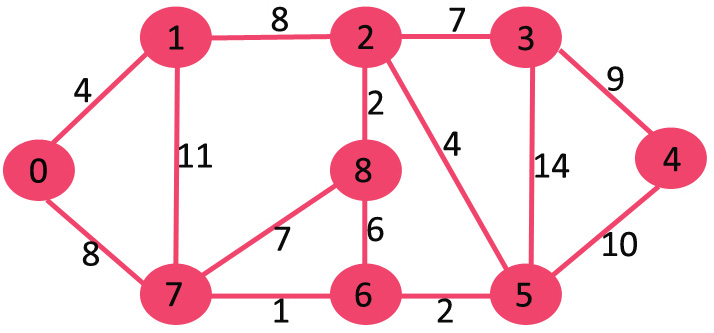
Djikstra's Algorithm
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks.
1) Create a set sptSet (shortest path tree set) that keeps track of vertices included in shortest path tree, i.e., whose minimum distance from source is calculated and finalized. Initially, this set is empty.
2) Assign a distance value to all vertices in the input graph. Initialize all distance values as INFINITE. Assign distance value as 0 for the source vertex so that it is picked first.
3) While sptSet doesn’t include all vertices
….a) Pick a vertex u which is not there in sptSet and has minimum distance value.
….b) Include u to sptSet.
….c) Update distance value of all adjacent vertices of u. To update the distance values, iterate through all adjacent vertices. For every adjacent vertex v, if sum of distance value of u (from source) and weight of edge u-v, is less than the distance value of v, then update the distance value of v.